|
 Megalithic
Quadrangles:
Megalithic
Quadrangles:
There are a handful
of megalithic structures in Europe which whilst retaining an essential
geometric design - are not circles. Remarkably, they also incorporate
a relationship between their dimensions, geometry, astronomy and the latitudes upon which
they were built.
As rare as they are,
megalithic quadrangles are found at some of the most significant
sites in Europe. The Station stones at Stonehenge are probably
the most famous, but quadrangles are also found at Carnac,
France; and near Evora, Portugal: All of which are areas of
megalithic and astronomical significance.
Although
Stonehenge is commonly known for
its solar orientation, the original construction has been identified
as having had a lunar orientation. In addition to this the site was constructed on the
exact latitude at which the maximum settings of the sun and moon are
at
90� to each other.
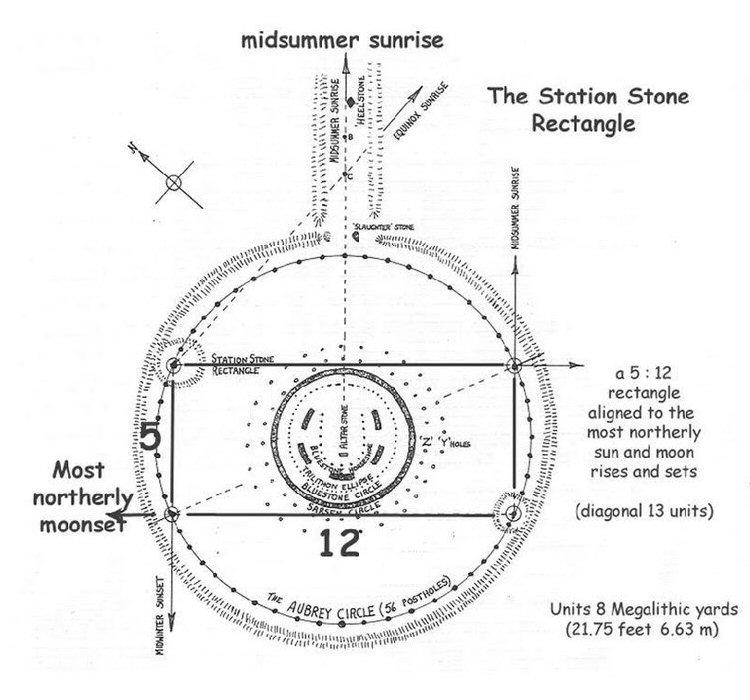
The smaller sides
of the Station-stone quadrangle are orientated at approximately
51� 10', which is the same as the latitude upon which it sits. The
sides of the rectangle were directed towards the maximum lunar and
solar settings. The Stonehenge quadrangle also encompasses the
second (5:12:13) Pythagorean triangle: Crucuno in France
encompasses the dimensions of the first set.
|
The Bush Barrow Lozenge:
This artefact was discovered
near Stonehenge, in the large Bush
Barrow, (c. 1,700 - 1,900 BC), which was excavated in
1808 by Sir Richard Colt Hoare and William Cunnington.
The barrow contained a male skeleton with rich funerary
goods, including a large 'lozenge'-shaped sheet of gold,
about 0.5 mm thick. The parallelogram (lozenge) measures
18 cm across and was placed on the dead mans chest.
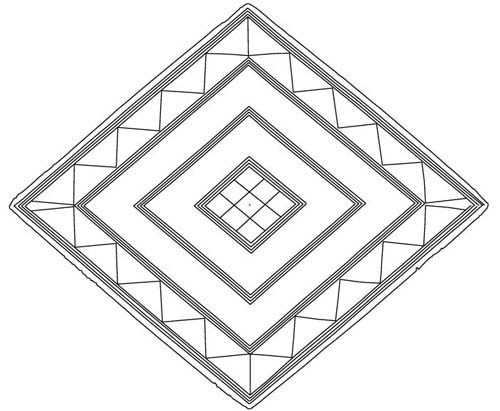
The redrawn and correctly scaled lozenge, based upon
measurements supplied by the Devizes Museum,
Wiltshire, England
(3)
It has been proposed that it could
have served as a solar and lunar calendar, using the
sight lines pointing in the direction of Sun solstices
and lunar standstills, as the angles on the lozenge are
the same as those produced by the sun and moon at their
extremes (1)
"By fixing the flat lozenge on a table at eye
level and orientating it with its shorter
diagonal on the meridian, an observer could use
an alidade while watching sunrise or sunset
throughout the year. Were the bronze rivets,
found nearby, the remains of the alidade?
Markings exist on the plaque which indicate that
the 16-month calendar was in use. Guide lines
exist for inserting the intercalary leap day.
Eight additional lines can be identified as
indicating moonrise and moonset at the
equinoxes' standstills".
(2)
|
(More about
Stonehenge)
Crucuno, France:
Crucuno is located at the unique latitude
on the Earth at which the solstice sun, both summer and winter,
form a perfect Pythagorean triangle relative to the parallel of
latitude, that is to the east-west, equinoxial axis of the site.
In turn, this 3:4:5 triangle is the first of the Pythagorean
triangular set.
The famous Carnac alignments in
France have at one end a stone-circle, and at the other a less
well known 'cromeleque' which is in-fact a quadrangular
enclosure. Prof. A. Thom determined that it was located at the unique latitude on the Earth at which the solstice
sun, both summer and winter, form a perfect Pythagorean triangle
relative to the parallel of latitude, that is to the east-west, equinoxial axis of the site. In turn, this 3:4:5 triangle is the first
of the Pythagorean triangular set.
Prof. A. Thom calculated that
the dimensions of Crucuno were 30 x 40 MY. This means that the
diagonal measures 50 MY, creating the first of the Pythagorean
triangles (3:4:5). The Stonehenge Station-stones encapsulate the
second in the set (5:12:13).
Burl
(8) said of this geometric
feature at Crucuno:
"It has been said
that the diagonals of the Crucuno rectangle indicate the rising
and setting points of the sun at the summer and winter solstices
(Charriere 1965). But such an arrangement for a 3 x 4 (or 30 x
40 MY) rectangle is only possible where certain unusual
conditions obtain. We shall proceed to explain these conditions.
First let us find
the latitude in which a 3x4 rectangle could be used to show the
sun rising and setting at both solstices. For zero true latitude
of the suns centre, we have the simple relation sin t = cos A
cos λ, where t is the suns declination at the solstice (i.e. the
obliquity of the ecliptic), A the azimuth and λ the latitude.
Since the Crucuno rectangle is 30 x 40 MY, cos A - 3/5 and so
cos λ - (5/8) sin c. If c = 23� 51' (the obliquity of the
ecliptic about 1,800 BC), λ - 47� 31'. It is remarkable that
this is so near the latitude of Crucuno 47� 37' ".
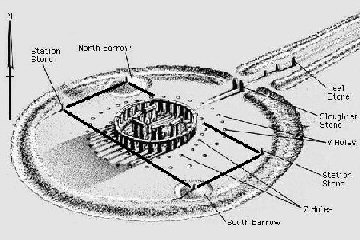

Quadrangular enclosures at Stonehenge
(left), and Crucuno (right).
Xarez, Portugal.
The
Xarez cromeleque
in Portugal is also a stone 'quadrangle'. Although the original layout
of the monument has been questioned, the archaeologist Dr. Pires Gon�alves
concluded after several years research on the site that its original
design was quadrangular. Perhaps of equal importance is the fact that
it belongs to an alignment of sites stretching over 50km, towards the
Almendres circle, with an azimuth
which closely conforms to the full moon in spring
(5).

The Xarez 'cromeleque', Monsaraz, Portugal.
(More about
the Xarez-Almendres Alignment)
Both Stonehenge and Almendres (Being two of the oldest and most
astronomically significant stone circles in Europe) are located on the latitudes of the extremes of
the moons 18.6 year cycle, such that at the latitude of 38.5� (Almendres)
the maximum declination the azimuth of moonrise would be 52.5� , while at
latitude 52.5� the extreme moonrise azimuth would be 38.5�, thereby
creating a relationship between the two latitudes. This calculation does not
take into account factors such as refraction or the variation in horizon
elevation or the changes caused by the passing of long periods of time and
at its worst is still remarkably only one degree of latitude out.
(More about
the Cromeleque da Xarez)
King Arthurs Hall, England.
Although
possibly just a coincidence, the cardinally orientated rectangular enclosure called
King Arthurs Hall in England is composed of 56 uprights, also suggestive of the
lunar count (18.6 x 3 = 55.8)
(Article by A. Whitaker, 2010)
(Stone
Circles)
(Archaeoastronomy)
|





